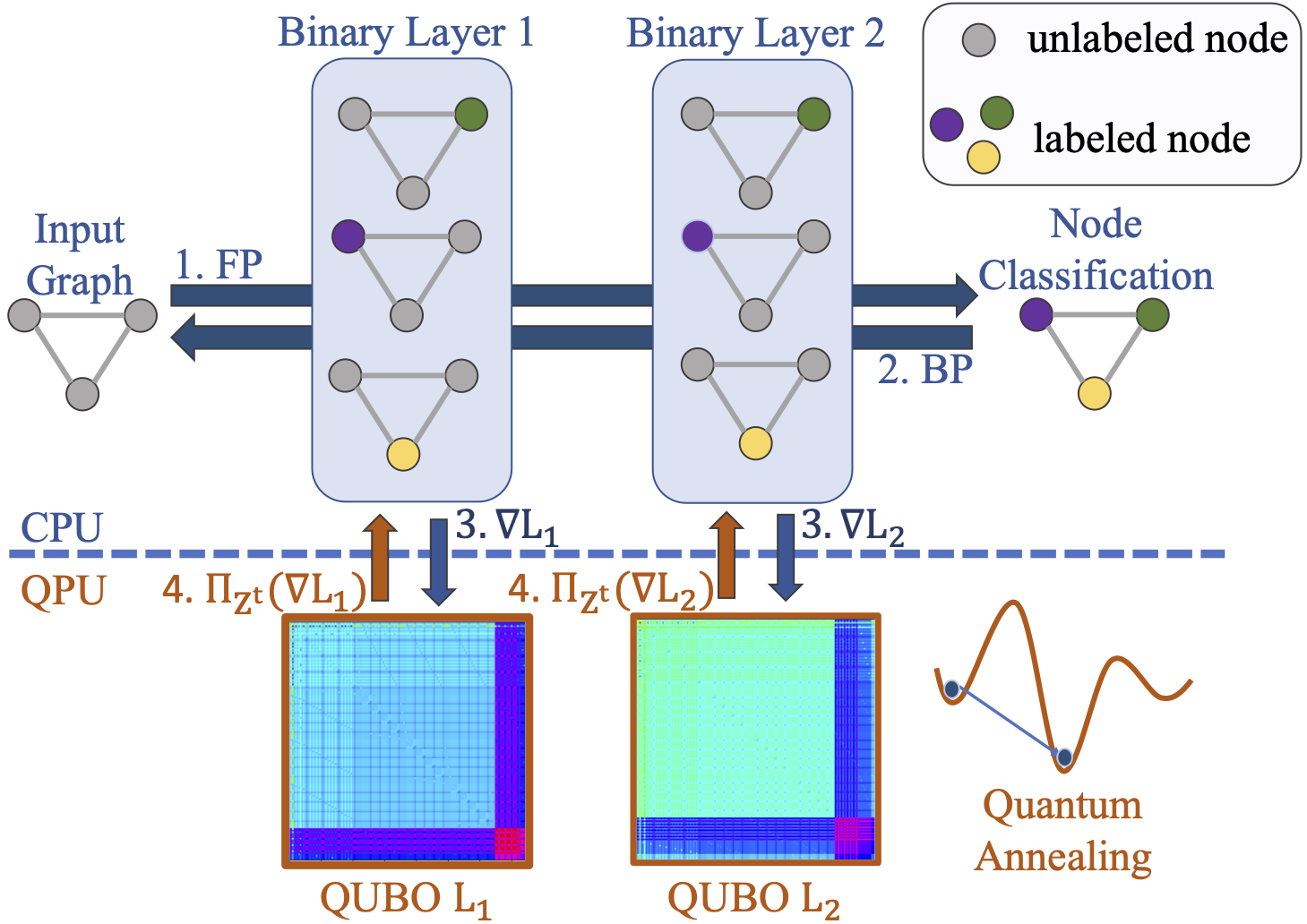
We present Quantum Projected Stochastic Binary-Gradient Descent (QP-SBGD), a novel per-layer stochastic optimiser tailored towards training neural networks with binary weights, known as binary neural networks (BNNs), on quantum hardware. BNNs reduce the computational requirements and energy consumption of deep learning models with minimal loss in accuracy. However, training them in practice remains to be an open challenge. Most known BNN-optimisers either rely on projected updates or binarise weights post-training. Instead, QP-SBGD approximately maps the gradient onto binary variables, by solving a quadratic constrained binary optimisation. Moreover, we show how the NP-hard projection can be effectively executed on an adiabatic quantum annealer. We prove that if a fixed point exists in the binary variable space, the updates will converge to it. Our algorithm is implemented per layer, making it suitable for training larger networks on resource-limited quantum hardware. Through extensive evaluations, we show that QP-SBGD outperforms or is on par with competitive and well-established baselines such as BinaryConnect, signSGD and ProxQuant when optimising binary neural networks.
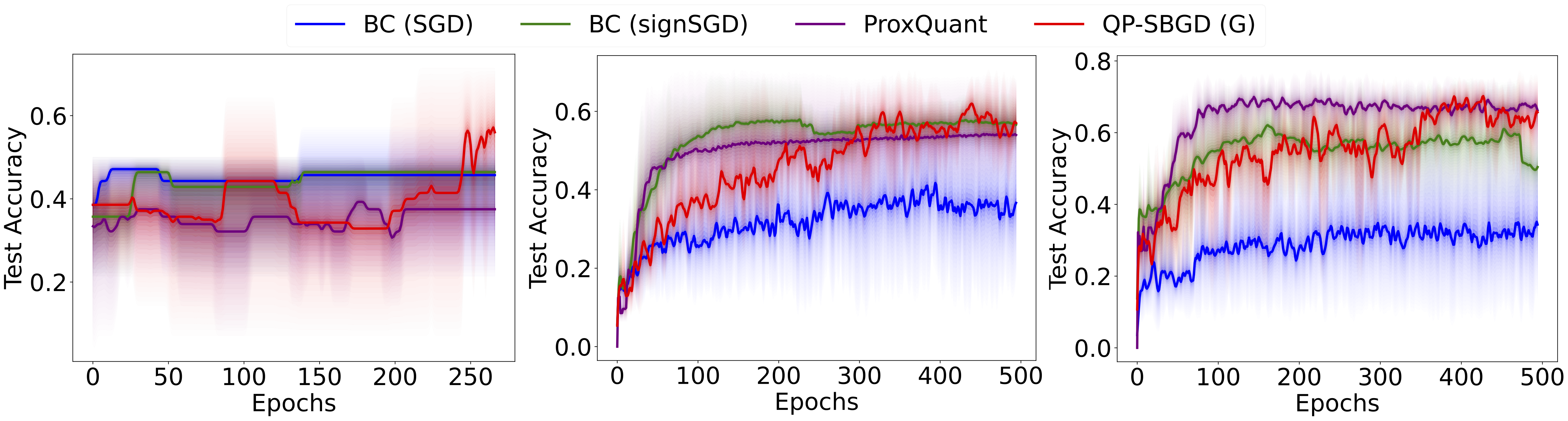
We use QP-SBGD to train binary graph convolutional neural networks. We compare the performance of QP-SBGD with BinaryConnect and ProxQuant on three datasets: Karate club, Cora and Pubmed. We report mean test accuracy over five runs. Overall we observe that QP-SBGD outperforms or is on par with the baselines.

We show the evolution of the QUBO formulation to calculate the weight updates for the first layer of a 2 layered binary neural network with the Quantum Projected Stochastic Binary-Gradient Descent algorithm. We display one QUBO after every 10th update. We observe here that all QUBOs have a rather densely connected support of the otherwise sparse graph. This overall sparsity of the graph enables us to embed those with minor embeddings and deploy them to the D-Wave QPU.


We show a few qualitative results on the MINIST digits dataset. We trained the network to classify the digits 1 and 2 with QP-SBGD (D-Wave). Similar to the numbers reported in the paper, the accuracy on those samples is 72.5%.
| ProxQuant | BC (SGD) | BC (signSGD) | QP-SBGD (Gurobi) | QP-SBGD (D-Wave) | |
|---|---|---|---|---|---|
| 0/2 | 0.65 | 0.64 | 0.71 | 0.66 | 0.62 |
| 1/2 | 0.67 | 0.72 | 0.66 | 0.73 | 0.70 |
| 1/7 | 0.64 | 0.74 | 0.68 | 0.75 | 0.74 |
We present the accuracy of the binary neural network on the MNIST dataset trained with different optimisers. We train the network to do a binary classification of the digit pairs (0,2), (1,2) and (1,7). Overall the QP-SBGD algorithm outperforms or is on par with the classical baseline, while being the first quantum deployable optimiser.
@article{krahn2024qpsgbd,
title = {Projected Stochastic Gradient Descent with Quantum Annealed Binary Gradients},
author = {Krahn Maximilian, Sasdelli Michele, Fengyi Yang Frances, Golyanik Vladislav, Kannala Juho, Chin Tat-Jun, Birdal Tolga},
year = {2024},
journal={BMVC}
}